Exascale computing, inexact modelling and geophysical applications: a conversation with Ernesto Bonomi
“Mega, giga, tera, peta, ...”
How many of us learned the refrain of the prefixes of the International System of Units while we were still at school? But technology is constantly evolving and now the old chant no longer seems to be adequate. The first 50 systems of the Top 5001 all come under the petascale computing league, the systems club with number-crunching performance greater than the petaflop/s, and two years have already gone by since the retirement of the IBM Roadrunner was decided, the earliest example of which for the first time, in 2008, reached the mythical performance of 1015 flop/s2 , 3 .
The new buzzword is exascale computing. To tell the truth, there is no shortage of reasons for scepticism. The Top 500 is there to remind us that we are still far from a factor of 20 or 30 for “exa-performance”, and there are those who would gamble their own money on the unattainability of this objective in the immediate future4. On the other side, that of the optimists, Intel is not hanging around and is pledging to provide an exascale computer by 20185.
There are many applications and lines of university and industrial research which are following this prospect closely and anxiously. One of the greatest challenges is in the field of geophysical exploration, which has put its trust in future computer systems with exascale performance to perfect software tools for the high-resolution “ecographic” reconstruction of the subsurface (seismic imaging): the identification and characterisation of ever-deeper and structurally complex reserves relies on these tools.
We are discussing this with Ernesto Bonomi, manager of the Energy and Environment sector of CRS4 and an expert in seismic imaging, a discipline traditionally associated with the use of computer systems on a massive scale. Earth sciences and, in particular, exploration for oil and gas are always amongst the leading drivers of high-performance computing technology, as is clearly explained in a recent community white paper from the sector6.
Ernesto, whose group has an ongoing multi-year scientific collaboration with the Exploration & Production division of Eni S.p.A., reels off a series of significant data. Progress in seismic acquisition technology has lead to the explosion in the quantity of data recorded – tens of terabytes for every campaign – whose transformation into an image of the subsurface via sophisticated algorithms, requires the use of considerable computing resources: tens of thousands of cores which provide computing resources in the order of petaflop/s. With the implementation of theoretical models of propagation which are ever closer to physical reality, the demand for computing is set to further increase, to reach the exaflop/s required for the reconstruction of the complex details of the deep subsurface in the next 5 to 10 years.
However, there is a practical limit to this expansion: the unsustainable electrical consumption caused by incremental jumps in clock frequency. The focus of high-performance computing is thus shifted from absolute computing power to the performance/energy consumption ratio measured in flop/s/W. With the denominator also appears the component required to dissipate the heat generated by the computing unit, a substantial part of the total7. Approximately speaking, the energy cost for the operation of a cluster becomes equal to that of purchase after about a year and a half. With the arrival of exascale computing, the demand for energy will rise dramatically (it is estimated by a factor of 103).
Today, the solution to curb this energy-intensive escalation involves the use of innovative HW architectures, such as GPGPU and FPGA, which accompany the traditional clusters of multicore CPUs. But there is a but: the programming model of the hardware accelerators is naturally aimed at data-parallel and data-flow paradigms which are often ill-adapted to implementation and to the solution of algebraic problems typical of digital simulation.
According to Ernesto, one of the challenges of the future will be the remodelling of the complexity of some problems, reformulating the physics of them and introducing minimal compromises to the accuracy of the solution, in order to tailor the solution algorithms as closely as possible to the hardware accelerators. In addition, this downsizing of the physical model combines naturally with the recent proposal to apply inexact computing to scientific modelling8 , 9 .
It is understood that not all problems can be reformulated in this manner: the identification of those which are suitable requires an accurate preliminary study. Among the many applications studied by his group (wave propagation in complex media, high-definition imaging, anisotropic elastic inversion of seismic data, gravimetric inversion at great depth), as a test case for this new approach, seismic imaging in the temporal domain was chosen: "By adopting a Lagrangian or corpuscular description of the wave front, the medium is modelled as a collection of refractory points each of which becomes the secondary source of a front which reaches the recording points on the surface with an angle of emergence and a curvature. From these two quantities, which are the unknowns to be determined, and which depend on the speed in the middle along the path of ascent, it is possible to calculate an approximation of the flight time of the signal and then identify, in the enormous volume of traces recorded, the useful events for the reconstruction of each point of the image" (further details in the Technical corner).
This reformulation has made it possible to move the problem of reconstructing ultrasound by solving a differential equation, which requires knowledge of the exact velocity field, to the characterization of the emerging wave fronts through the simultaneous solution guided by the data from a multitude of optimisation problems, one for each point in the image. The new strategy has proven successful, since i) the flow of calculation and data generated by the optimisation algorithms and the imaging is perfectly suited to the paradigms of the data-parallel programming and data-flow from the new hardware accelerators; ii) the first comparisons with the standard commercial software, which implement the conventional strategy, have given more than satisfactory results in real complex cases, both in terms of accuracy and of S / N ratio. The prototype developed has therefore been able to take the first step toward industrialization.
There is an argument to which Ernesto attaches great importance: training, which is also shared by the researchers: “The application of extreme computing to seismic imaging and other problems of Energy & Environment requires a sophisticated cocktail of mathematical knowledge, IT skills and geophysical culture which cannot be expected of a recent graduate. Post-graduate training courses would be necessary for this, taught by the researchers at CRS4 who work at first hand on these issues.”
Thus, we confidently await exascale computing. And in the meantime, we will take care of the training of new generations of researchers who will make future supercomputers their everyday working tools.
— F. Maggio
Technical corner10
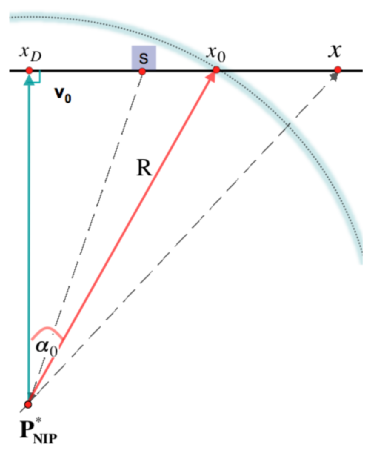
In a 2D medium with known near-surface velocity \(V_0\), the response of \(P_{NIP}\), a point modeled as a diffractor, is considered (NIP = Normal Incidence Point)11. The objective is to approximate the traveltime with respect to a reference ray which is carried to the surface by a diffraction wavefront with radius of curvature \(R\) and emerging with an elevation angle \(\alpha_0\). In an auxiliary homogeneous medium with velocity \(V_0\), the resulting trace \(x_0\) approximates a hypothetical coincident source-receiver recording12 with a two-way time of flight \(2R/V_0\) (see Figure 1).
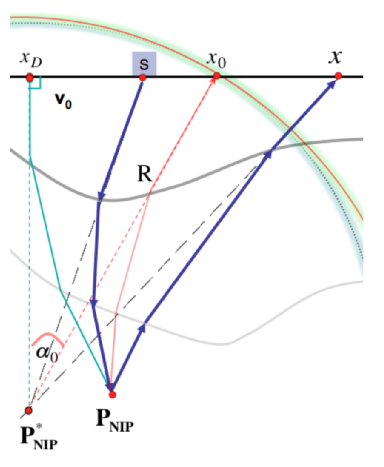
In 2D one can introduce the osculating circle to give a circular approximation of the diffraction wavefront, as illustrated in Figure 2: the center \(P^{\ast}_{NIP}\) of the osculating circle tangent to the front in \(x_0\) - the reference emergence point - becomes in the auxiliary medium the image point of \(P_{NIP}\). Assuming a constant velocity \(V_0\) near the surface in both media, within the circular approximation it is difficult to distinguish whether \(P^{\ast}_{NIP}\) or \(P_{NIP}\) has originated the diffraction front. The time of flight of a ray reaching the acquisition plane at a point of coordinate \(x\) with respect to the reference ray \(x_0\), \(\alpha_0\) is given by the Pythagoras’ theorem:
| \(t_A(x-x_0) = \frac{1}{V_0}\sqrt{R^2 \cos^2 \alpha_0 + \left [ x-x_0 + R \sin \alpha_0 \right ]^2}\) |
(1) |
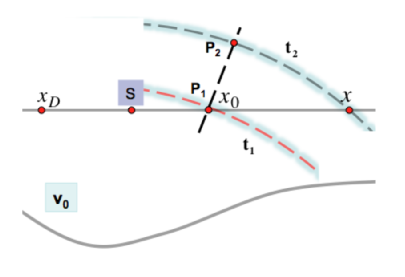
Given a point \(x\) close enough to \(x_0\), such that the two points are swept respectively at times \(t_2\) and \(t_1\) by the circular approximation of the true perturbation (see figure 3), one has that \(|t_2-t_1| \simeq \overline{P_2 P_1}/V_0\) which gives rise to the following approximation, known as \textit{homeomorphic transformation}:
| \(t_A (x - x_0 ) - t_A (0) \simeq t (x - x_0) - t(0)\) |
(2) |
where, from (1), \(t_A (0)=R/V_0\). The idea behind time migration is strictly linked with the concept of image ray, the ray that after leaving a buried diffracting point, emerges vertically to the acquisition plane at position \(x_D\) after a two-way traveltime \(t_D\). Time migration means stacking all diffracted events common to \(P_{NIP}\) to form, at the \((x_D,t_D)\) location of the image section, a representation of the diffracting point. Since, approximately, the image ray leaving \(P_{NIP}\) is the one which minimizes \(t(x-x_0)\), the following relations hold true:
| \(x_D \simeq x_0 - R \sin \alpha_0 \ , \ \ t_D \simeq t_0 - \frac{4R}{V_0} \sin^2 \left ( \frac{\alpha_0}{2} \right )\) |
(3) |
The mapping between \((x_0,t_0)\) and \((x_D,t_D)\) coupled with equation (1) brings to \(t_M(x-x_D)\), the traveltime associated with the image ray and such that \(t_M(0)=t_D/2\). Thus, the traveltime between a generic source-receiver pair can be written as
| \(\tau_D(x_S-x_R) \simeq t_M(x_S-x_D) + t_M(x_R-x_D)\) |
(4) |
which provides an explicit expression of traveltimes in the prestack domain with respect to \((x_D,t_D)\), a point in the migrated domain. More in details, equations (3) along with the field of attributes \(\xi(x_0 ,t_0) = \left \{\alpha_0 (x_0 ,t_0 ), R(x_0 ,t_0) \right\}\) establishes the following correspondence between the \((x_0 ,t_0 )\)-section and the \((x_D ,t_D)\)-section: if \(P_{NIP}\) lies on a reflector, there can be only one admissible reference ray, the normal-incidence one that reaches the surface at a specific coordinate \(x_0\); if \(P_{NIP}\) is a diffractor, there are an infinite number of reference rays and as many values of \(x_0\). In any case, there will be only one image point at the position \((x_D,t_D)\) of the migrated volume.
The numerical values of attributes \(\xi\) can be evaluated by maximizing the fitness between the actual arrival times of seismic events and the diffraction traveltimes , thus the semblance coefficient
| \(S\left(\xi|x_0,t_0 \right) = \frac{1}{M} \, \frac{\Sigma_{k=-N/2}^{N/2} \left | \Sigma_{i=1}^M a_{i,\tau^{(i)}+k}\right |^2}{\Sigma_{k=-N/2}^{N/2} \Sigma_{i=1}^M \left | a_{i,\tau^{(i)}+k}\right |^2}\) |
(5) |
where \(a_{i,j}\) denotes the \(j\)-th temporal sample along the \(i\)-th trace belonging to the midpoint-offset aperture imposed by \(x_0\) and \(t_0\). As the derivatives of (5) are not explicitly available, a suitable conjugate-direction optimizer (with no need of gradient) along with a reliable line search algorithm are adopted. Maximization of the semblance coefficient (5), concurrently repeated for each point \(P_{NIP}\), provides fields of attributes \(\xi_{opt}\) that can be used either to stack seismic traces or to migrate them. Three possibilities exist:
- if \(P_{NIP}\) is a diffractor, all traveltimes of the optimized surface correspond to events which, once averaged, interfere constructively and form an image either at point \((x_0,t_0)\) or, via mapping (3), at \((x_D,t_D)\);
- if \(P_{NIP}\) is a reflector, averaging over all events, only those governed by Snell’s law interfere constructively and form an image either at point \((x_0,t_0)\) or, via mapping (3), at \((x_D,t_D)\);
- if \(P_{NIP}\) is neither a diffractor nor a reflector, the optimized traveltime does not correspond to meaningful events and, averaged, they interfere destructively.
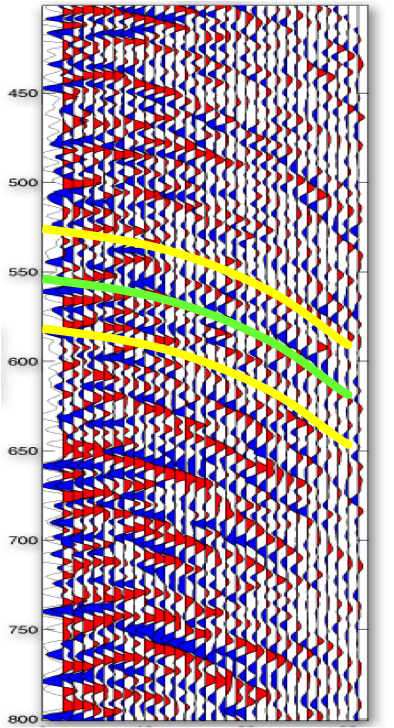
Figures 4 and 5 illustrate how the maximization of the semblance coefficient is used to find the most adequate travel time parameters, and the time-migration of a synthetic Earth model, respectively.
The generalization of this quasi-similar earth models to the 3D case is more complex but feasible by introducing the pair of emergence angles \( \left (\alpha_0 , \beta_0 \right ) \) and the two principal curvatures of the diffraction front reaching the surface at \(x_0\) in time \(t_0\) .
The implementation has demonstrated that it is possible to move time imaging from the solution of the partial differential equation that models the medium response, into a data-driven optimization problem. This work represents an important step in seismic imaging and has opened new perspectives on data processing, in both isotropic and anisotropic media.
Homage to Samuel Barclay Beckett (Dublin, 13 April 1906 – Paris, 22 December 1989)
November 2014. Next list will be published in June 2015 ↩
http://arstechnica.com/information-technology/2013/03/worlds-fastest-supercomputer-from-09-is-now-obsolete-will-be-dismantled/ ↩
http://www.extremetech.com/computing/155941-supercomputing-director-bets-2000-that-we-wont-have-exascale-computing-by-2020 ↩
http://www.exascale-computing.eu/wp-content/uploads/2012/02/Exascale_Onepager.pdf ↩
Hwang L, Jordan T, Kellogg L, Tromp J et al, “Advancing solid earth system science through high-performance computing”, white paper, 2014 ↩
Pop E, “Energy Dissipation and Transport in Nanoscale Devices”, Nano Research, 3, 147, 2010 ↩
http://www.nytimes.com/2015/05/12/science/inexact-computing-global-warming-supercomputers.html?smprod=nytcore-iphone&smid=nytcore-iphone-share ↩
Duben P, Joven J, Lingamneni A, McNamara H et al, “On the use of inexact, pruned hardware in atmospheric modeling”, Phil. Trans. R. Soc. A, 372, 2014 ↩
Bonomi E, Caddeo G, Cristini A, Marchetti P, “Data-driven time imaging of 2D acoustic media without a velocity model'', in Proceedings of 82nd Annual Meeting and International Exposition of the Society of Exploration Geophysics-SEG, Las Vegas - Nevada (USA), 2012 ↩
For a basic introduction to seismic migration, see for instance the AAPG Wiki http://wiki.aapg.org/Seismic_migration ↩
Bonomi E, Tomas C, Marchetti P, Caddeo G, “Velocity-independent and data-driven prestack time imaging: It is possible!", The Leading Edge, 33(9), 1008-1014, 2014 ↩