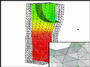
L’obiettivo di questa linea di ricerca è lo studio e l’implementazione di tecniche di visualizzazione appropriate per dati di elementi finiti in due e tre dimensioni. In particolare, ci occupiamo di situazioni “insolite” come discontinuità di campo e celle deformate. Tali dati sono prodotti, ad esempio, da simulazioni chimiche, da simulazioni fluidodinamiche o, in generale, ovunque sia richiesta un’elevata precisione nella descrizione del dominio di confine. I metodi degli elementi finiti sono particolarmente adatti a rappresentare i processi fisici nei programmi di simulazione. Diverse applicazioni nel campo della fluidodinamica richiedono la rappresentazione di campi discontinui definiti su celle di elementi finiti. Tali dati sono prodotti, ad esempio, come output di processi di simulazione chimica. La combinazione di metodi di simulazione a elementi finiti discontinui, griglie topologicamente non strutturate e approssimazioni di alto ordine di campi e geometrie consente ai programmi di gestire una varietà di situazioni in cui gli approcci standard solitamente falliscono. In particolare, le griglie strutturate presentano notevoli limitazioni quando si tratta di geometrie complesse o quando si cerca di adattarsi alle caratteristiche locali della soluzione. Inoltre, i metodi degli elementi finiti discontinui garantiscono l’accuratezza temporale della soluzione da ottenere utilizzando approssimazioni polinomiali di ordine elevato all’interno di ciascun elemento (cella), risultando quindi particolarmente adatti alle griglie non strutturate. Infine, quando un programma di simulazione agli elementi finiti richiede un’elevata precisione nella descrizione dei confini del dominio computazionale, è spesso necessario trattare celle geometricamente deformate, poiché la forma non lineare di queste celle può fornire un’approssimazione dei confini migliore rispetto a una forma lineare. Gli approcci di visualizzazione comuni non offrono la possibilità di gestire le discontinuità e questo ambito di ricerca sembra essere completamente inesplorato quando le discontinuità sono combinate con una topologia non strutturata.
Lo scopo della nostra ricerca è fornire strumenti di visualizzazione generici per rappresentare mesh costituite da celle topologicamente diverse (una combinazione di triangoli, quadrilateri e altri poligoni convessi generici nel caso bidimensionale; una combinazione di tetraedri insieme a esaedri e poliedri convessi generici nel caso tridimensionale) su cui sono definiti campi scalari discontinui. Inoltre, la descrizione parametrica non lineare della geometria deve essere rappresentata graficamente insieme ai valori di campo definiti su di essa. Approssimazione polinomiale di ordine elevato Tutti gli strumenti e le tecniche di visualizzazione standard si basano sul presupposto che ogni variabile definita su una cella abbia un comportamento lineare. Uno dei problemi principali da affrontare è l’approssimazione lineare della funzione polinomiale ai fini del rendering. Nel nostro approccio, tale linearizzazione è stata eseguita utilizzando l’algoritmo Longest Side Midpoint Insertion, un metodo iterativo in cui ad ogni passo ogni cella non direttamente linearizzabile, rispetto a una stima di errore definita e a una soglia data, viene divisa lungo il suo lato più lungo in due celle. Questo metodo ha dimostrato di convergere in un numero finito di iterazioni verso un’approssimazione lineare della funzione definita sulla mesh originale, dato un valore di tolleranza, sia nello spazio 2D che 3D. Rappresentazione della discontinuità Una rappresentazione efficiente delle discontinuità è un problema importante da risolvere per la visualizzazione degli elementi finiti discontinui. La discontinuità è un’informazione fondamentale nel processo di simulazione: la discrepanza nei valori delle funzioni alle interfacce delle celle fornisce informazioni sulla convergenza della soluzione. A tal fine abbiamo deciso di trattare ogni cella come un’entità separata, rappresentando il valore della funzione in ogni vertice indipendentemente dal valore delle altre celle che condividono quel vertice. Questo modo di descrivere la soluzione effettiva è stato poi combinato con la rappresentazione della soluzione media ottenuta calcolando per ogni vertice il valore della funzione nella cella ad esso incidente. La possibilità di descrivere sia la soluzione effettiva che quella media si rivela un ottimo modo per enfatizzare le discontinuità. Entrambe le soluzioni sono rappresentate mediante tecniche di visualizzazione classiche (ovvero isocontorni e mappatura dei colori), come descritto nella sezione seguente. Un altro approccio per la rappresentazione delle discontinuità consiste nel mappare la varianza della soluzione discontinua sui bordi della griglia sottostante. In questo modo le discontinuità diventano evidenti all’interno della mesh e la loro visualizzazione può essere combinata con isocontorni o mappatura cromatica della soluzione effettiva o media. Anche per la geometria non lineare, durante la visualizzazione di questo tipo di dati, il problema risiede nella rappresentazione delle celle deformate con primitive grafiche lineari. L’obiettivo è quello di fornire una buona approssimazione di tali celle con un insieme di celle lineari. Stiamo valutando la possibilità di applicare l’inserimento del punto medio del lato più lungo anche in questo caso. Il lavoro di ricerca alla base degli algoritmi di visualizzazione è stato parzialmente finanziato dalle autorità regionali sarde. Un primo risultato pratico della nostra ricerca è l’implementazione di un sistema di visualizzazione per la rappresentazione di campi discontinui definiti su griglie non strutturate. Il sistema, denominato MIGAVIS, combina diverse tecniche per rappresentare le discontinuità su topologie non strutturate all’interno di una semplice interfaccia utente parametrica. Il sistema è attualmente utilizzato presso ENEL di Pisa (Polo Termico) come strumento di visualizzazione efficiente per dati discontinui basati sull’analisi degli elementi finiti ottenuti da processi di simulazione di flussi compressibili e viscosi. MIGAVIS è stato sviluppato potenziando il Visualization Toolkit (VTK) orientato agli oggetti di Schroeder, Martin e Lorensen con nuove classi per la gestione delle informazioni di linearizzazione e discontinuità. L’applicazione è stata completamente sviluppata in C++ e la piattaforma di sviluppo è una workstation Silicon Graphics IRIX 5.3. Un’interfaccia utente parametrica implementata in OSF/Motif consente una facile interazione con i dati. Il sistema offre la possibilità di visualizzare: la griglia in wire-frame su cui è definita la soluzione; la soluzione discontinua effettiva; la soluzione media. Sia la soluzione effettiva che quella media possono essere descritte tramite una rappresentazione scalare (tramite isocontorni o mappatura dei colori) o una rappresentazione vettoriale (tramite glifi o ricci). L’utente può selezionare in modo interattivo il campo scalare (cioè una soluzione specifica corrispondente a una variabile nel processo di simulazione) per la visualizzazione scalare e/o i campi scalari per la visualizzazione vettoriale. La visualizzazione vettoriale si ottiene semplicemente combinando diverse soluzioni scalari. La varianza della soluzione può essere mappata sulla griglia dei bordi ogni volta che lo si desidera, enfatizzando così i valori discrepanti alle interfacce delle celle proprio in corrispondenza della loro posizione all’interno della griglia. Tutte queste visualizzazioni possono essere combinate per produrre un’unica immagine. Il sistema di visualizzazione è integrato in un’interfaccia che offre la possibilità di modificare in modo interattivo i parametri del processo di visualizzazione, ovvero: parametri per il processo di linearizzazione; mappe cromatiche per la varianza e per tutte le rappresentazioni delle soluzioni e delle griglie; intervalli di valori per la varianza e per tutte le rappresentazioni delle soluzioni; numero di contorni; parametri dei glifi e degli hedgehog (altezza, scala, ecc.); parametri per mappe cromatiche lineari e non lineari; fattore di scala per gli assi cartesiani; fattore di offset per gli oggetti visualizzati rispetto agli assi cartesiani.
Chiudi