Exascale computing, inexact modelling e applicazioni alla geofisica: intervista con Ernesto Bonomi
“Mega, giga, tera, peta, ...”
In quanti abbiamo imparato il ritornello dei prefissi del Sistema Internazionale sui banchi di scuola? Ma la tecnologia incalza e oggi la vecchia cantilena sembra non bastare più. I primi 50 sistemi della Top5001 rientrano tutti nella petascale computing league, il club dei sistemi con performance di number crunching superiore al petaflop/s, e due anni sono ormai passati da quando è stato deciso il pensionamento di IBM Roadrunner, il capostipite che per primo, nel 2008, raggiunse la mitica performance dei 1015 flop/s2 , 3 .
La nuova parola d'ordine è exascale computing. A dire la verità i motivi di scetticismo non mancano. La Top500 è lì a ricordarci che siamo ancora lontani di un fattore 20 o 30 dalla “exa-performance”, e c'è chi scommette di tasca propria sulla non fattibilità di questo obiettivo nel futuro immediato4 . Sull'altro fronte, quello degli ottimisti, Intel ha rotto gli indugi impegnandosi a fornire un computer exascale entro il 20185 .
Sono molte le applicazioni e i filoni di ricerca universitaria e industriale che guardano con attenzione e ansia verso questa prospettiva. Una delle grandi sfide è posta dall’esplorazione geofisica che fa affidamento sui futuri sistemi di calcolo con performance exascale per il perfezionamento degli strumenti software di ricostruzione “ecografica” ad alta risoluzione del sottosuolo (imaging sismico): su questi strumenti
si basano l’identificazione e la caratterizzazione di giacimenti sempre più profondi e strutturalmente complessi.
Di questo parliamo con Ernesto Bonomi, responsabile del settore Energy and Environment del CRS4 ed esperto di imaging sismico, una disciplina tradizionalmente legata all'uso di sistemi di calcolo di grandissima scala. Le scienze della terra e, in particolare, la prospezione Oil&Gas sono da sempre tra i leading drivers delle tecnologie di calcolo ad alta prestazione, come ben spiegato in un recente “community white paper” del settore6 . Ernesto, il cui gruppo vanta una collaborazione scientifica ormai pluriennale con la divisione Exploration & Production di Eni S.p.A., snocciola una serie di dati significativi. Il progresso nelle tecnologie di acquisizione sismica ha condotto all’esplosione della quantità di dati registrati - decine di TeraByte per ogni campagna - la cui trasformazione in un’immagine del sottosuolo mediante algoritmi sofisticati richiede l’utilizzo di risorse computazionali ingenti: decine di migliaia di core che assicurano prestazioni di calcolo dell’ordine dei petaflop/s. Con l’implementazione di modelli teorici di propagazione sempre più vicini alla realtà fisica, la richiesta di calcolo è destinata ad aumentare ulteriormente, fino a raggiungere nei prossimi 5-10 anni gli exaflop/s necessari alla ricostruzione dei dettagli complessi del sottosuolo profondo.
Esiste però un limite pratico a questa espansione: l’insostenibile consumo elettrico causato dai salti incrementali di frequenza di clock. Il focus del calcolo ad alta prestazione è dunque spostato dalla potenza di calcolo assoluta al rapporto performance/consumo energetico misurato in flop/s/W. Al denominatore compare anche la componente necessaria per la dissipazione del calore generato dalle unità di calcolo, una frazione consistente del totale7 . Approssimativamente, il costo energetico per il funzionamento di un cluster diventa uguale a quello di acquisto dopo circa un anno e mezzo. Con l'avvento dell'exascale computing la richiesta energetica salirà drammaticamente (si stima di un fattore 103).
Oggi la ricetta per arginare questa escalation energivora prevede l'uso di architetture HW innovative, come GPGPU e FPGA, che affiancano i tradizionali cluster di CPU multicore. Ma c'è un ma: il modello di programmazione degli acceleratori hardware è naturalmente orientato verso paradigmi data-parallel e data-flow che sovente si adattano male all’implementazione e alla soluzione di problemi algebrici tipici della simulazione numerica.
Secondo Ernesto una delle sfide per il futuro sarà la rimodulazione della scala di complessità di alcuni problemi, riformulandone la fisica e introducendo compromessi minimi con l’accuratezza della soluzione, così da potere ritagliare al meglio gli algoritmi risolutivi sugli acceleratori hardware. È un’idea che si abbina in modo naturale con la proposta recente di applicare l’inexact computing al modelling scientifico8 , 9 .
Resta inteso che non tutti i problemi possono essere ripensati in tal senso: l'individuazione di quelli adatti richiede un accurato studio preliminare. Tra le numerose applicazioni studiate dal suo gruppo (propagazione d'onda in mezzi complessi, imaging ad alta definizione, inversione elastica anisotropa di dati sismici, inversione gravimetrica ad alta profondità), come banco di prova per questo nuovo approccio è stato scelto l'imaging sismico nel dominio temporale: “Adottando una descrizione lagrangiana o corpuscolare del fronte d’onda, il mezzo viene modellato come una collezione di punti diffrattori ciascuno dei quali diventa la sorgente secondaria di un fronte che raggiunge i punti di registrazione in superficie con un angolo di emergenza e una curvatura. A partire da queste due quantità, che sono incognite da determinare e che dipendono dalla velocità nel mezzo lungo il percorso di risalita, è possibile calcolare un’approssimazione del tempo di volo del segnale per poi identificare, nell’enorme volume di tracce registrate, gli eventi utili alla ricostruzione di ciascun punto dell’immagine” (ulteriori dettagli nel Technical corner).
Questa riformulazione ha permesso di spostare il problema della ricostruzione ecografica dalla soluzione di un’equazione differenziale, che richiede la conoscenza del campo di velocità esatto, alla caratterizzazione dei fronti d’onda emergenti attraverso la soluzione concorrente guidata dai dati di una moltitudine di problemi di ottimizzazione, uno per ciascun punto dell’immagine. La nuova strategia si è dimostrata vincente, poichè i) il flusso di calcolo e di dati generato dall’algoritmo di ottimizzazione e di imaging si adatta perfettamente ai paradigmi di programmazione data-parallel e data-flow dei nuovi acceleratori hardware; ii) i primi confronti con software commerciali di riferimento, che implementano la strategia convenzionale, hanno dato risultati più che soddisfacenti su casi reali complessi sia in termini di accuratezza che di rapporto S/N. Il prototipo sviluppato ha potuto perciò fare il primo passo verso l'industrializzazione.
C'è un argomento a cui Ernesto attribuisce una grande importanza: la formazione, svolta anche in affiancamento ai ricercatori: “L'applicazione dell'extreme computing all'imaging sismico e ad altri problemi di Energy & Environment richiede un cocktail sofisticato di conoscenze matematiche, skills informatici e cultura geofisica che non si può richiedere ad un neolaureato. Per questo sarebbero necessari corsi di formazione post-laurea tenuti dai ricercatori del CRS4 che lavorano in prima persona su queste tematiche.”
Aspettiamo fiduciosi l'exascale computing, dunque. E nel frattempo curiamo la formazione delle nuove generazioni di ricercatori, che dei futuri supercomputer faranno il loro strumento di lavoro di tutti i giorni.
— F. Maggio
Technical corner10
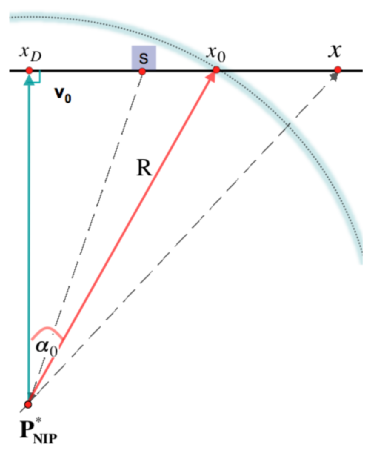
In a 2D medium with known near-surface velocity \(V_0\), the response of \(P_{NIP}\), a point modeled as a diffractor, is considered (NIP = Normal Incidence Point)11. The objective is to approximate the traveltime with respect to a reference ray which is carried to the surface by a diffraction wavefront with radius of curvature \(R\) and emerging with an elevation angle \(\alpha_0\). In an auxiliary homogeneous medium with velocity \(V_0\), the resulting trace \(x_0\) approximates a hypothetical coincident source-receiver recording12 with a two-way time of flight \(2R/V_0\) (see Figure 1).
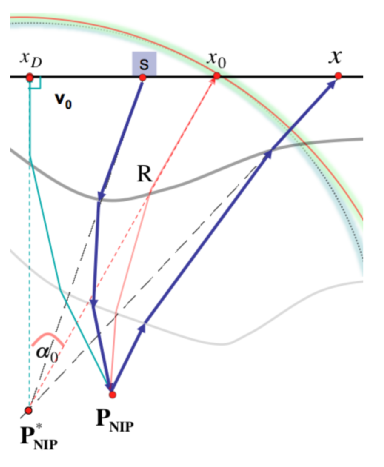
In 2D one can introduce the osculating circle to give a circular approximation of the diffraction wavefront, as illustrated in Figure 2: the center \(P^{\ast}_{NIP}\) of the osculating circle tangent to the front in \(x_0\) - the reference emergence point - becomes in the auxiliary medium the image point of \(P_{NIP}\). Assuming a constant velocity \(V_0\) near the surface in both media, within the circular approximation it is difficult to distinguish whether \(P^{\ast}_{NIP}\) or \(P_{NIP}\) has originated the diffraction front. The time of flight of a ray reaching the acquisition plane at a point of coordinate \(x\) with respect to the reference ray \(x_0\), \(\alpha_0\) is given by the Pythagoras’ theorem:
| \(t_A(x-x_0) = \frac{1}{V_0}\sqrt{R^2 \cos^2 \alpha_0 + \left [ x-x_0 + R \sin \alpha_0 \right ]^2}\) |
(1) |
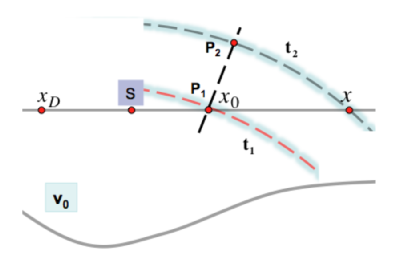
Given a point \(x\) close enough to \(x_0\), such that the two points are swept respectively at times \(t_2\) and \(t_1\) by the circular approximation of the true perturbation (see figure 3), one has that \(|t_2-t_1| \simeq \overline{P_2 P_1}/V_0\) which gives rise to the following approximation, known as \textit{homeomorphic transformation}:
| \(t_A (x - x_0 ) - t_A (0) \simeq t (x - x_0) - t(0)\) |
(2) |
where, from (1), \(t_A (0)=R/V_0\). The idea behind time migration is strictly linked with the concept of image ray, the ray that after leaving a buried diffracting point, emerges vertically to the acquisition plane at position \(x_D\) after a two-way traveltime \(t_D\). Time migration means stacking all diffracted events common to \(P_{NIP}\) to form, at the \((x_D,t_D)\) location of the image section, a representation of the diffracting point. Since, approximately, the image ray leaving \(P_{NIP}\) is the one which minimizes \(t(x-x_0)\), the following relations hold true:
| \(x_D \simeq x_0 - R \sin \alpha_0 \ , \ \ t_D \simeq t_0 - \frac{4R}{V_0} \sin^2 \left ( \frac{\alpha_0}{2} \right )\) |
(3) |
The mapping between \((x_0,t_0)\) and \((x_D,t_D)\) coupled with equation (1) brings to \(t_M(x-x_D)\), the traveltime associated with the image ray and such that \(t_M(0)=t_D/2\). Thus, the traveltime between a generic source-receiver pair can be written as
| \(\tau_D(x_S-x_R) \simeq t_M(x_S-x_D) + t_M(x_R-x_D)\) |
(4) |
which provides an explicit expression of traveltimes in the prestack domain with respect to \((x_D,t_D)\), a point in the migrated domain. More in details, equations (3) along with the field of attributes \(\xi(x_0 ,t_0) = \left \{\alpha_0 (x_0 ,t_0 ), R(x_0 ,t_0) \right\}\) establishes the following correspondence between the \((x_0 ,t_0 )\)-section and the \((x_D ,t_D)\)-section: if \(P_{NIP}\) lies on a reflector, there can be only one admissible reference ray, the normal-incidence one that reaches the surface at a specific coordinate \(x_0\); if \(P_{NIP}\) is a diffractor, there are an infinite number of reference rays and as many values of \(x_0\). In any case, there will be only one image point at the position \((x_D,t_D)\) of the migrated volume.
The numerical values of attributes \(\xi\) can be evaluated by maximizing the fitness between the actual arrival times of seismic events and the diffraction traveltimes , thus the semblance coefficient
| \(S\left(\xi|x_0,t_0 \right) = \frac{1}{M} \, \frac{\Sigma_{k=-N/2}^{N/2} \left | \Sigma_{i=1}^M a_{i,\tau^{(i)}+k}\right |^2}{\Sigma_{k=-N/2}^{N/2} \Sigma_{i=1}^M \left | a_{i,\tau^{(i)}+k}\right |^2}\) |
(5) |
where \(a_{i,j}\) denotes the \(j\)-th temporal sample along the \(i\)-th trace belonging to the midpoint-offset aperture imposed by \(x_0\) and \(t_0\). As the derivatives of (5) are not explicitly available, a suitable conjugate-direction optimizer (with no need of gradient) along with a reliable line search algorithm are adopted. Maximization of the semblance coefficient (5), concurrently repeated for each point \(P_{NIP}\), provides fields of attributes \(\xi_{opt}\) that can be used either to stack seismic traces or to migrate them. Three possibilities exist:
- if \(P_{NIP}\) is a diffractor, all traveltimes of the optimized surface correspond to events which, once averaged, interfere constructively and form an image either at point \((x_0,t_0)\) or, via mapping (3), at \((x_D,t_D)\);
- if \(P_{NIP}\) is a reflector, averaging over all events, only those governed by Snell’s law interfere constructively and form an image either at point \((x_0,t_0)\) or, via mapping (3), at \((x_D,t_D)\);
- if \(P_{NIP}\) is neither a diffractor nor a reflector, the optimized traveltime does not correspond to meaningful events and, averaged, they interfere destructively.
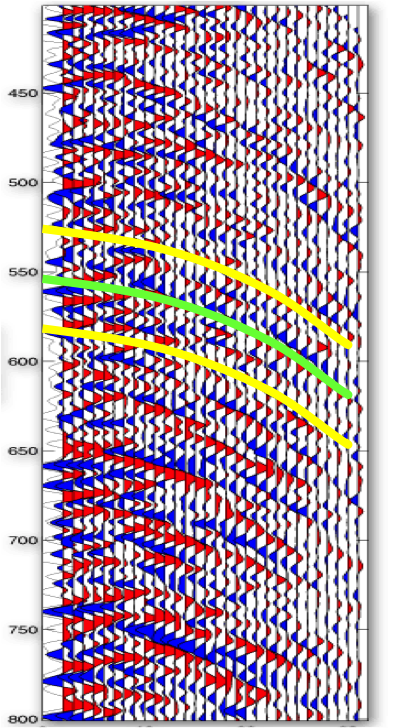
Figures 4 and 5 illustrate how the maximization of the semblance coefficient is used to find the most adequate travel time parameters, and the time-migration of a synthetic Earth model, respectively.
The generalization of this quasi-similar earth models to the 3D case is more complex but feasible by introducing the pair of emergence angles \( \left (\alpha_0 , \beta_0 \right ) \) and the two principal curvatures of the diffraction front reaching the surface at \(x_0\) in time \(t_0\) .
The implementation has demonstrated that it is possible to move time imaging from the solution of the partial differential equation that models the medium response, into a data-driven optimization problem. This work represents an important step in seismic imaging and has opened new perspectives on data processing, in both isotropic and anisotropic media.
Homage to Samuel Barclay Beckett (Dublin, 13 April 1906 – Paris, 22 December 1989)
Novembre 2014. La prossima graduatoria sarà pubblicata a giugno 2015 ↩
http://arstechnica.com/information-technology/2013/03/worlds-fastest-supercomputer-from-09-is-now-obsolete-will-be-dismantled/ ↩
http://www.extremetech.com/computing/155941-supercomputing-director-bets-2000-that-we-wont-have-exascale-computing-by-2020 ↩
http://www.exascale-computing.eu/wp-content/uploads/2012/02/Exascale_Onepager.pdf ↩
Hwang L, Jordan T, Kellogg L et al, “Advancing solid earth system science through high-performance computing”, white paper, 2014 ↩
Pop E, “Energy Dissipation and Transport in Nanoscale Devices”, Nano Research, 3, 147, 2010 ↩
http://www.nytimes.com/2015/05/12/science/inexact-computing-global-warming-supercomputers.html?smprod=nytcore-iphone&smid=nytcore-iphone-share ↩
Duben P, Joven J, Lingamneni A, et al, “On the use of inexact, pruned hardware in atmospheric modeling”, Phil. Trans. R. Soc. A, 372, 2014 ↩
Bonomi E, Caddeo G, Cristini A, Marchetti P, “Data-driven time imaging of 2D acoustic media without a velocity model'', in Proceedings of 82nd Annual Meeting and International Exposition of the Society of Exploration Geophysics-SEG, Las Vegas - Nevada (USA), 2012 ↩
For a basic introduction to seismic migration, see for instance the AAPG Wiki http://wiki.aapg.org/Seismic_migration ↩
Bonomi E, Tomas C, Marchetti P, Caddeo G, “Velocity-independent and data-driven prestack time imaging: It is possible!", The Leading Edge, 33(9), 1008-1014, 2014 ↩