Today there is so much information around us that it is hard to organize and benefit from it in a rational way. We need an innovative approach to the problem. Which one? We ask Hanan Samet, who is visiting CRS4.
Some time ago I was sipping a coffee at the bar of CRS4 with a friend. «That's a new colleague, an expert in databases», I observed, pointing at the person. Sporting his usual English humor, my friend replied: «A database is a table of rows and columns. How can one be an expert in a table?». My friend had in mind a relational1 model database. It is an idea that dates back to the '70s of the last century - shortly after the appearance of the first "modern" computers - whose importance lies, of course, not in the table itself but rather in the possibility to perform operations on the contents, from the elementary ones concerning creation, read, update, and deletion (CRUD) to the more sophisticated SCRUD which also includes search.
Today's society, with newspapers, TV, radio, the Web, and social networks, is totally imbued with informative contents. For now, digital storage of this contents does not seem to be an insurmountable problem for current technology. After all, this is the raison d'être for databases, isn't it? Among others, coupled with the original idea of a two-dimensional table, more sophisticated multidimensional2 as well alternative models, optimized for specific tasks, have also been proposed. We will not dwell on this but, for the non-expert readers, we point out two interesting contributions, one in favor of the hotshots on the horizon, the NoSQL (Not Only SQL) models3, and the other in defense of "traditional" models4. These technological armaments, well-supported by the availability of high performance hardware, are doing their job. Geographic data. Images. Protein catalogues. The Web. These are just some of the many examples of data arising more and more frequently in the applied sciences and technology in a world of increasing complexity, like ours, represented and manipulated efficiently with databases of various kinds.
And here we are confronted with the real issue: how can we extract - in a targeted and intelligent way - the required information from this plethora5 of data? The current approach, keyword-based, requires the use of one or more keywords (with the possible exclusion of other keywords, and the indication of the type of resource sought, etc). Often, however, the user is not able to specify the exact keywords because he has only a partial idea of the search object. In these cases, one would definitely appreciate a search engine that is able to work also "by approximation" using synonyms or, to put it in more technical jargon, capable of proximity searches as well as of keyword matching. Another feature that is now hard to give up, is "granularity": to overcome the difficulties of visualization and navigation in an endless sea of information, it makes sense to start the search by selecting one of a limited number of generic options offered by the search engine, and then refining the query iteratively, once the proposed options will become more specific.

Today we meet someone who offers an effective solution to these problems: his idea is to index spatial attributes (such as the coordinates on a map, a piecewise linear curve approximating a road or a river, or a rectangular area defining a geographic region) in a database and to make search engines that query it more powerful and flexible. Of course, if you are looking for the latest articles on the solution of the 3D bidomain equations using finite volumes (key search words: "bidomain equations" "finite volumes" 3D -monodomain filetype:pdf), then you are probably not interested in specifying whether the place of publication is New Zealand rather than Milan or Boston. In other words, the spatial granularity is not so fundamental to the query (you do not expect hundreds of thousands of articles on the subject). However, for topics which are more general and more relevant to our daily lives, the locations associated with them are important and hence a map query interface can make a difference. This is also because many of us have in our pocket something potentially capable of measuring (and transmitting) spatial attributes related to our movements: our GPS-enabled smartphones6. Very likely, spatial attributes will become more and more common and increasingly present in the near future.
Our guest, Hanan Samet, is an undisputed guru in the field of multi-dimensional and spatial data structures and mathematical techniques for sorting spatial information. His book "Foundations of multidimensional and metric data structures"7 is a must have for anyone involved in search algorithms of spatial data in computer graphics, visualization, GIS, image processing, computer vision, game programming, and beyond. Hanan, who got his Ph.D. from Stanford University in 1975 and is currently a Distinguished University Professor at the University of Maryland, as well as being ACM Distinguished Speaker, has received an impressive number of academic awards8 including the ACM Paris Kanellakis Theory and Practice Award as well as the IEEE Computer Society's Wallace McDowell Award. We met him9 thanks to Enrico Gobbetti and Fabio Bettio from the Visual Computing Lab of CRS4.
Professor Samet, it is a great pleasure to meet you here at CRS4. Why here?
I am here to deliver a series of three seminars in the ACM Distinguished Lecture Series organized by CRS410: this is one of the initiatives of the European project DIVA11, led by Enrico Gobbetti from CRS4 and Renato Pajarola from the University of Zurich, focused on the visualization and analysis of large volumes of data. In addition, I have come to meet Enrico Gobbetti and researchers of the Visual Computing Lab at CRS4, and to see in greater detail the results of their work. It's the first time I visit their center and I was impressed both by the results of research in Visual Computing, which are absolutely at the international level, and by the wide variety of practical applications. In addition to the lab, I visited, for example, the installation at the National Archaeological Museum of Cagliari for the interactive exploration of the Mont'e Prama statuary [we'll talk about in a very short time, stay tuned!].
You are a well-known expert in multidimensional and metric data structures and the use of databases to store such data. Why are these kind of data structures and databases so important, especially in comparison to the ones that are used in traditional relational databases?
Actually, traditional relational databases can be used to store multidimensional data12 as each record in a relational database can be viewed as a point in a multidimensional space. The issue is that some multidimensional data such as spatial data aside from point data such as individual locations is different in that it has extent (e.g., aggregates of locations such as line segments, regions, surfaces, and volumes). For example, line segments can be transformed into points in a higher dimensional space by just recording the coordinate values of their endpoints. However, this transformation does not preserve proximity [see the Technical Corner] as two line segments that are close to each other in the space from which they are drawn may not be close to each other in the transformed higher dimensional space which makes search inefficient as the transformed space is much larger than the space from which they are drawn. As we know, we encounter locations and collections thereof (e.g., trajectories for paths) in daily applications once we use our GPS-enabled devices such as our smartphones. The efficient representation of the data is crucial to the utility of the devices. Of course, there is also the issue of privacy in terms of whether we want our locations to be divulged to others such as service providers, but this is another topic that is beyond the scope of my visit.
Which are, nowadays, the most popular applications of multidimensional and metric data structures?
They are certainly very much used in similarity searching, for example to search for the nearest neighbors in machine learning and other applications where the ultimate goal is to find those objects that are similar to the query object. These data structures allow you to use a non-traditional meaning of the concept of sorting, expanding on the usual meaning of an order which means using a mono-dimensional index. The key idea is that we are interpreting the term sorting as the action of differentiating among the objects. Of course, it is possible to sort the data by mapping the multidimensional spatial attributes (e.g., the coordinate values) into a 1D space through a linear mapping. Our differentiation action is accomplished by sorting the data with respect to the space that it occupies. This is like bucketing or imposing a grid on the underlying space to facilitate access as is often the case with the map indexes with which we are all familiar.
Today, computer graphics plays a key role in the sciences, engineering, education, medicine, media and other applications, and generally requires serious computing power. What are the biggest challenges for computer graphics and why are hierarchical representations so important?
Well, invariably the operations that are performed involve searching, and the way to accelerate this task is to "organize" the data, usually through sorting. This can be seen by noting that many algorithms in computer graphics involve the key questions of "given a location, which features are there?" or "given a feature or event, where does it take place?". Obviously we are not always aware of this process, but that is what happens in practice.
In your book you present a large number of methods for the sorting of spatial data, such as those based on a decomposition of the underlying space and those that use object hierarchies with minimum bounding rectangles which may or may not be disjoint. It is a crowded zoo. Why so many methods and how can we choose the one that best suits our applications?
In fact, as I often like to say, there are two families of methods, one based on a hierarchy of objects and one based on a hierarchy of cells: surprisingly, this is not always understood. Moreover, the problems often arise from different application areas. So, different people try to solve them in different ways. In my book, I make an attempt to show the similarity of apparently different methods. So, yes, there are a number of techniques but often they are related to one another.
How have data structures changed over time with respect to the early models, proposed almost 40 years ago? Some, like quadtrees and their variants, are still used. Is this a surprise for you?
Not really. I think that many people did not understand how applicable and general these methods are. The issues have changed over time and also the methods to address them have evolved in parallel. For instance, applications like video games and location-based services are now commonly used and they make use of data structures such as quadtrees, while in the past quadtrees were considered exotic objects used only by those who did image processing. Today with smartphones, spatial attributes are no "different" from the other data. In such cases, for example, knowledge of where events take place is important information: so location can be an effective way to index the events. Given an appropriate interaction device, I don't need to know exactly what I'm looking for: I can indicate a point on a map, zoom in, move, and view the information associated with certain spatial coordinate values. For example, if I'm looking for a rock concert in Manhattan and if I find one in Harlem, then it's a good result, because Harlem is contained in Manhattan; but also a rock concert in Brooklyn is likely to fit my query, because it is a reasonably nearby sibling borough, although not exactly matching my query. Lastly, if the result is an event in New York City, then this is quite generic in the sense that New York City contains Manhattan, but is still better than no result. These distinctions are more important than you might think. In particular, if you use a traditional search engine and type in non exact keywords, then you will probably not find the event in which you are interested; on the contrary, the search for location allows a significant flexibility. Obviously, this makes it necessary to implement an index based on location and use appropriate data structures.
Along with your coworkers, you developed NewsStand13, an application for browsing information and news by location. Could you explain us how it works?
The most important aspect is that it enables me to search for events whose details I do not know beforehand: selecting a location on the map, I can decrease the scale to get more detail, pan the map, and see what happened in which place, and only then make my choice. Of course you can also perform keyword searches, for instance concerning a well-defined event, and NewsStand will indicate the location or locations where this event took or will take place. The detail of information and events provided by NewsStand depends on the geographical scale selected: a local event concerning Sardinia is probably not shown when the user views the entire globe, but instead becomes visible when the search is performed on a more local geographic scale. In other words, NewsStand works according to a "granularity" principle to locate information and events.
The innovative idea of NewsStand is to make the map the querying medium of choice: it is an approach that can be extended to documents other than the news (e.g., you've developed TwitterStand, whose targets are obvious from the name). What do you consider the most promising fields of application in the near future?
I think it will be possible to access more and more information through location: photos, tweets, etc. Generally any object with an ontology and a spatial attribute can be inserted into a multidimensional database, explorable via map-type queries, based on geographic information. One type of research which in my view is very appealing is associated with time-based queries. Take for example the spread of a disease like Ebola: the appearance of the virus will likely be mentioned in the local media, and thanks to the information contained in the news database it will be possible to reconstruct the evolution over space and time of the epidemic and the history of its propagation. Another important application for companies is to identify the geographical areas where a particular brand is mentioned, more or less often in the newspapers, TV, Web, and other media. For example, this can help to plan rational advertising, rather than making generalized campaigns that may be more expensive and less effective. Moreover, it is often useful for embassies to collect mentions in local news media concerning the country of origin and return them to their central government. These are all examples of investigations, typically made by human experts, which NewsStand could dramatically accelerate.
A very impressive idea you faced in the course of your research work14 is the attempt to predict the characteristics of future events, using the information of the recent past and present. Can you tell us more about this topic?
It's a good question. Think about the previous example of the disease propagation: I can try to compute the future pattern of distribution of the epidemic from the recent trend. It is a very general topic: it covers both events which are much discussed in the media but also unexpected events. The applications are obvious, such as for resource planning or to minimize the risks related to natural events which may be catastrophic (for example, predicting where a hurricane will strike). It is a natural direction for future research that can have evident benefits for society.
Will you work in this direction? More generally, how do you choose your research topics? And which is your relationship with companies dealing with such data?
[Smiles] Much of my work depends on whether or not I find students interested to work on a particular topic. This is a general problem of research: you can have a good idea, but then you have to convince others. You can not force anyone to work on something that they do not believe in. As I like to say, you can lead a horse to water but you can not make it drink it. The relationship with companies is not easy. In general they have a short-term vision of what can be done. We do not have much financial support for our students from companies. Also, we must always be aware of the "elephant in the room", the company most famous in the world for what concerns search engines. Most people believe that this company has solved all existing problems related to search and manipulating all data. However, this is not true for all data and topics. There still remain many topics of research and important open problems to be tackled and solved in the next years.
— F. Maggio
Technical Corner
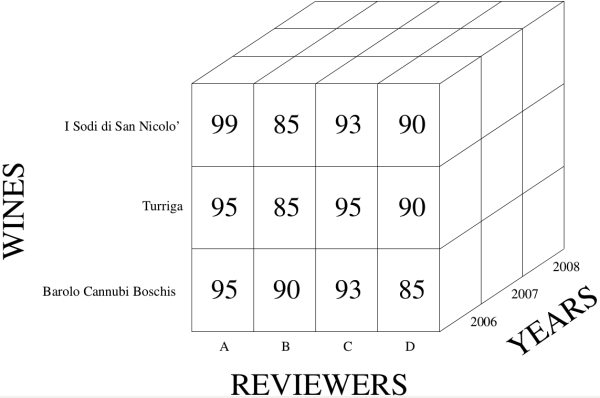
While "classical" realational databases rely on a 2D traditional row and column structure, multidimensional databases result from using a hypercube representation, where each dimension is associated with an object attribute. As an illustration, consider the example below consisting of the ratings of three leading Italian red wines presented using both a relational (Table 1) and a multidimensional database (Figure 1).
| Table 1. Scores of three leading Italian red wines using a relational database | ||||||||
|---|---|---|---|---|---|---|---|---|
| id | wine | producer | year | Aa | Bb | Cc | Dd | total |
| 11 | I Sodi di San Nicolò | Castellare di Castellina | 2006 | 99 | 85 | 93 | 90 | 367 |
| 14 | Turriga | Argiolas | 2006 | 95 | 85 | 95 | 90 | 365 |
| 21 | Barolo Cannubi Boschis | Luciano Sandrone | 2006 | 95 | 90 | 93 | 85 | 363 |
| a Gambero rosso, http://www.gamberorosso.it/vini b L'Espresso, http://goo.gl/UYOQCI c Veronelli, http://www.seminarioveronelli.com d Luca Maroni, http://lucamaroni.com |
||||||||
Let us now suppose that we want to add more data to our red wine database, say the ratings of these wines for the years 2007 and 2008. In the case of a relational database, a simple way to do this is to add 3 new rows to Table 1 for each of the two additional years. Alternatively, we can represent the same information using the multidimensional database shown in Figure 1:
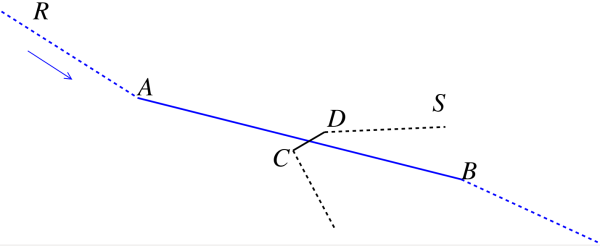
From now on, we no longer dwell on the difference between relational and multidimensional databases (often refered to as models) as either one or the other model can be used for representing spatial data - the actual object of our interest -, by simply setting the appropriate attributes. For instance, the spatial attributes for a line segment representing a portion of a road or a river, consist of 2 pairs of \((x,y)\) coordinate values15 of their endpoints, resulting in either 4 columns in a table or a point in a 4-dimensional real space. Independently of the model adopted, the representation of spatial data has a well-known problem: indexes commonly used for query and look up in non spatial databases are not well-suited for manipulation and search of spatial datasets. In fact, while traditional indexes do a great job when simple retrieval of data is needed, they have serious drawbacks with spatial queries: one of the most important being that they do not preserve proximity16. For example, consider the situation depicted in Figure 2, where segments \(AB\) and \(CD\) are part of the representation of a river \(R\) and a road \(S\), respectively, and one wants to query if \(S\) is near \(R\) or, even more importantly, if \(S\) crosses \(R\).
Actually, given a simple representation of a segment \(AB\) in terms of the coordinate values of its endpoints, the metric distance in a 4-dimensional space between the segments is clearly an unreliable indicator of the proximity of the two spatial objects. This representation shows a major issue in practical queries with spatial data which is that it only identifies the space spanned by the data objects (e.g., all of the points that make up the line segment), information which is not feasible to provide explicitly. For example, it is not practical for the database to store the names of all of the roads that pass through each point in the underlying space, or equivalently to store the name of every road that crosses every river.
Such considerations motivated researchers to introduce new index types, complying with proximity preservation, and often based on suitable mathematical structures like trees to speed up access to the underlying data. The obvious idea is to separate the non-spatial components, which can be handled in a standard way, from the spatial components which deserve special indexing treatment. A comprehensive introduction and analysis of the different spatial index types may be found in the previously mentioned book of Hanan Samet. Here we limit ourselves to summarizing the main features of the most important families of such methods, without going into too much detail. The basic idea is to decompose the space to which the data belong into regions called buckets. There are several ways to do that.
-
Object hierarchies with minimum bounding rectangles (MBRs)
In this case we aggregate the group of objects into collections of distinct subgroups of a finite size which are recursively aggregated so the the result is a tree.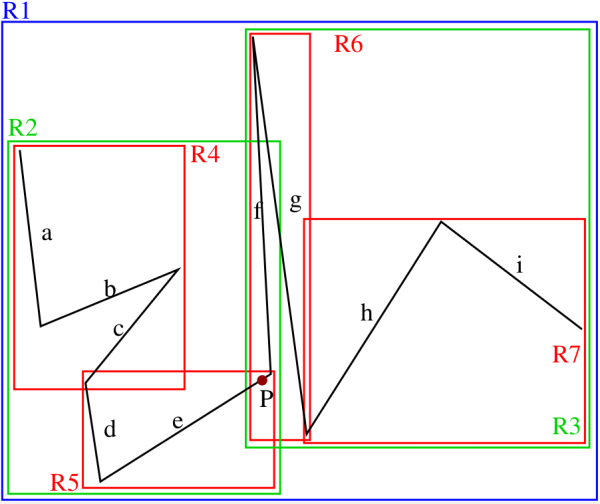
Figure 3. A piecewise linear curve represented by an object hierarchy with minimum bounding rectangles (MBRs). Note the introduction of some empty space in order to enable the illustration of the boundaries of the MBRs which are actually coincident as is the case, for example, for the right boundaries of R3 and R7 as well as for the right and the left boundaries of R6 and R7, respectively. Adapted from 16 The fact that the objects can be arbitrarily-shaped means that operations such as point lookup (i.e., if a point is contained in an object) or object intersection detection can be complex and thus we simplify such tests by associating a minimum bounding box (e.g., rectangle, sphere, etc.) with each object or object aggregate as now the operation involves one or two known shapes. This approach is primarily used with rectangle minimum bounding boxes (known as MBRs), and here we restrict ourselves to the two-dimensional case. The result is a non-disjoint decomposition of the underlying space as the MBRs can overlap. This means that the area spanned by a single object (e.g. a line segment) may be included in multiple MBRs, even if each object is associated with just one MBR. The R-tree and the R*-tree are examples of data structures that belong to the object hierarchy family. An example of the space decomposition induced by an R-tree for a piecewise linear curve is shown in Figure 3.
Figure 4 is the tree structure corresponding to the R-tree of Figure 3. Notice the presence of overlapping MBRs in Figure 3. This means that when, for example, we want to determine which line segment contains a particular point, we may have to search the entire underlying space as the point may lie in several MBRs even though the line segment object on which it lies is associated with only one MBR. In other words, we must examine all of the MBRs in which the point lies. For example, the line segment containing point P in Figure 3 is included in MBRs R2, R3, R5,and R6, while it actually only belongs to R5.
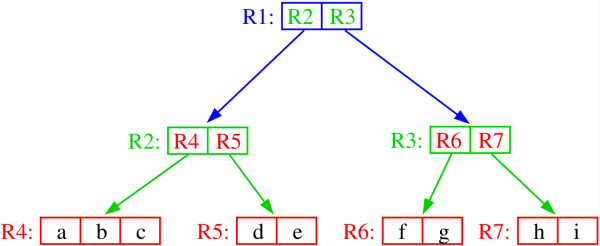
Figure 4. The R-tree associated with the MBR object hierarchy of Figure 3. Adapted from 16 -
Decomposition of the embedding space
In this case, we focus on methods that decompose the space in which the objects are embedded (and hence also the objects) into disjoint non-overlapping cells. There are many variants of such methods. One such method starts with an object hierarchy that employs MBRs such as the R-tree discussed in the previous section and then decomposes the MBRs into disjoint cells so that they span the space that contains the objects. The R\(^+\)-tree and the cell tree are examples of it. As objects are split into several parts (i.e., sub-objects), such methods generally take up more space than the method that uses an object hierarchy with the complete MBR. However, this enables the more efficient performance of many operations including those that find the object that contains a particular point, as there is no need to traverse the entire object collection. Figure 5 is the disjoint cell analog of the piecewise linear curve of Figure 3.
Figure 5. A piecewise linear curve represented by disjoint cells. Note the introduction of some empty space in order to enable the illustration of the boundaries of the MBRs which are actually coincident as is the case, for example, for the right boundaries of R3 and R7 as well as for the right and the left boundaries of R6 and R7, respectively. Adapted from 16 Figure 6 is the tree structure corresponding to the R\(^+\)-tree of Figure 5. Comparing Figure 6 with Figure 4 we see that some of the objects appear more than once in Figure 6 while this is never the case in Figure 4.
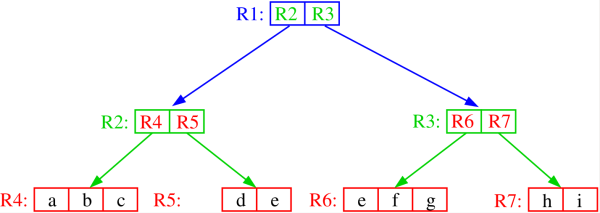
Figure 6. The R\(^+\)-tree associated with the disjoint cells model of Figure 5. Adapted from 16 The quadtree family of representations is a very different example of the methods that decompose the embedding space. In this case the embedding space is usually decomposed recursively into 4 congruent cells (assuming without loss of generality that the underlying space is two-dimensional) until some property of the relationship between the objects and cells is satisfied. For example, one stopping condition in the case of two-dimensional region data is that each cell is a member of at most just one region. In this case, the quadtree is an alternative to the bitmap representation as shown in Figure 7.
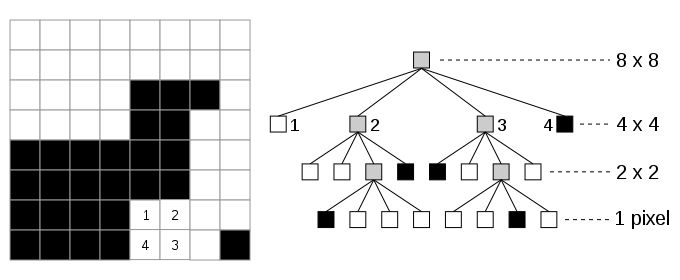
Figure 7. A 2D bitmap (left) and its quadtree representation (right). Numbers 1,2,3,4 indicate indexing order of children. Attribution: Wojciech Muła, via Wikimedia Commons More generally, quadtrees can be used to represent various types of spatial data. One common use is to represent a collection of point data (e.g. cities on a map) where the cell is decomposed if it has more than \(k\) objects where the cell is like a bucket and \(k\) is the bucket capacity. Figure 8 is an example of the decomposition of the underlying space induced by such a quadtree for a collection of European cities with a bucket capacity of 1. This variant of the quadtree is known as a PR quadtree where P and R denote point and region, respectively. In this case, the leaf nodes are either empty or contain just one point object along with the coordinate values of the point (not shown in the figure).
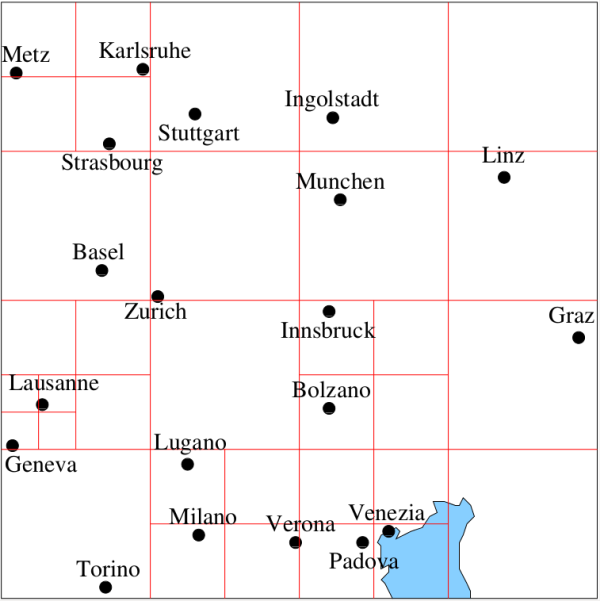
Figure 8. Map of a few European cities subdivided following a quadtree decomposition rule with a bucket capacity of 1. Note that object in close proximity (e.g. Geneva and Lausanne) may result in a finer decomposition of the underlying space and hence a deeper tree structure. See 1617 Figure 9 is the tree representation of the quadtree structure for the collection of European cities in Figure 8. The leaf nodes are represented by either white square (empty nodes) or black ones (nodes containing data). A major drawback of this implementation is that points in close proximity may result in deep trees (e.g., see the cities of Lausanne and Geneva in this example). This problem can be overcome by setting the bucket capacity to a value \(c>1\).
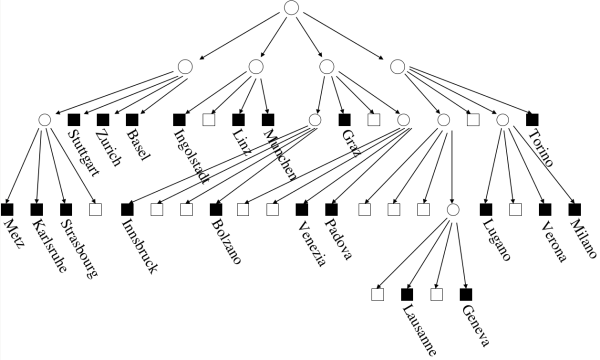
Figure 9. The tree representation of the quadtree associated with the European cities dataset. The numbering order of the subtrees is the same as in Figure 7. Quadtrees are especially well-suited for location-based queries which is the case that we are given a location and that we want to know what features or objects are associated with it.
-
There are considerably many more methods for indexing spatial data that space constraints prevent us from reviewing. Among them is the pyramid, whose internal nodes contain a summary of the information in the nodes below them, which allows us to skip nodes with no relevant information when performing a search query. The pyramid performs well with feature-based queries which correspond to the case that we are given a feature or an object and we seek to know which locations are associated with it (also known as spatial data mining)18.
Other interesting methods include octrees, partition fieldtrees, hierarchical decompositions by triangles or rectangles, etc. For a detailed review of these techniques we refer to the already mentioned book of Hanan Samet7 and the associated spatial data structure applets19.
The reference in the title is so celebrated that we need add no further details. Instead, we take the chance to remember a former colleague and friend who left us a few days ago. This focus is a homage to Gianfranco Frau (Cagliari 1974, Cagliari 2015).
Actually a relational database may consist of multiple linked tables which, along with a suitable manipulation system (RDBMS), should comply with strictly defined rules, described in Codd EF, A relational model of data for large shared data banks, Communications of the ACM, 13, 6:377-387, 1970 and subsequent technical papers. We do not linger over this topic ↩
The latter are based on hypercube representation, where all similar information is grouped along the same axis, making search operations easier. See the Technical Corner for more details. The multidimensional model better reflects the intrinsic structure of a dataset: the relationships between the various data are more obvious and the operations of manipulation of the objects are in general more performing, see for example Collins J, An assessment of multi-dimensional databases and their use, http://goo.gl/Bf1Ze0, 2003 ↩
Oliver AC, Which freaking database should I use?, InfoWorld, http://goo.gl/YYRRJQ, 2012 ↩
Sotnikov D, Don’t write off relational databases for big data just yet, ReadWrite, http://goo.gl/1sw95, 2013 ↩
For an example of a spatial database and the operations that it can support, see Samet H, Alborzi H, Brabec F, Esperança C, Hjaltason GR, Morgan F, and Tanin E, Use of the SAND spatial browser for digital government applications, Communications of the ACM, 46(1):63-66, 2003 ↩
Other consumer electronics products are moving in this direction; see, for example, the geotagging feature of the latest cameras ↩
By H. Samet, Morgan Kauffman Publishers, 2006, http://goo.gl/Oh2rkS ↩
The interview was conducted on 22/07/2015 by myself and Andrea Mameli at the Is Molas Hotel in Pula, whom we thank for hosting us. We also wish to thank Hanan for the effort he has devoted to improving this focus, including the English style and grammar. ↩
It is important to stress the difference between multidimensional databases (as opposed to relational ones, see the Technical Corner) and multidimensional data. ↩
http://newsstand.umiacs.umd.edu/web/. Also see the article Samet H, Sankaranarayanan J, Lieberman MD, Adelfio MD, Fruin BC, Lotkowski JM, Panozzo D, Sperling J and Teitler BE, Reading news with maps by exploiting spatial synonyms, Communications of the ACM, 57(10):64-77, 2014 found at http://tinyurl.com/newsstand-cacm as well as the accompanying video at http://vimeo.com/106352925 ↩
Ho S, Lieberman M, Wang P and Samet H, Mining future spatiotemporal events and their sentiment from online news articles for location-aware recommendation system, Proceedings 1st ACM MobiGIS, 2012, 25-32 ↩
We assume a flat Earth approximation ↩
Samet H, A sorting approach to indexing spatial data, International Journal on Shape Modeling, 14(1):15-37, 2008 ↩
Samet H, Sorting in space: multidimensional, spatial, and metric data structures for computer graphics applications, in ACM SIGGRAPH 2008 classes, 2008, ACM New York, 90, 1-106 ↩
Aref WG, Samet H, Efficient processing of window queries in the pyramid data structure, in Proceedings of the 9th ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems (PODS), Nashville, TN, 1990, 265-272 ↩


